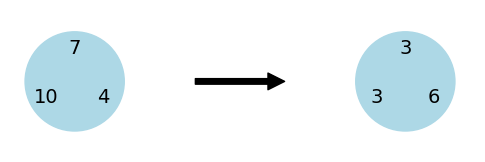
Take any vector with real numbers as entries, say ![]() and produce new vector, namely
and produce new vector, namely ![]() . You can imagine it as having the numbers in cirlce, going clockwise and taking differences. Then iterate this operation. The sequence of vectors we obtain is called Ducci sequence.
. You can imagine it as having the numbers in cirlce, going clockwise and taking differences. Then iterate this operation. The sequence of vectors we obtain is called Ducci sequence.
For example if we set ![]() and take
and take ![]() , we obtain this sequence
, we obtain this sequence ![]() and we got a cycle with period
and we got a cycle with period ![]() .
.
Convergence is obviously the thing one will think about as one of the very first things. There are some nice results we will explore, for example that any n-tuple converges to some multiple of vector with entries only from ![]() . We will call vectors like these “binary vectors”. Our first step will be to understand proof of this claim.
. We will call vectors like these “binary vectors”. Our first step will be to understand proof of this claim.
Because it converges to vector like that and we will care about vectors with integer inputs, we will know for sure we actually get to multiple of vector with inputs only with inputs from ![]()
Actually if we have multiple of binary vector, we can without loss of generality just work with the binary vector itself. If ![]() is this binary vector, then
is this binary vector, then ![]() after applying Ducci operation will be vector in form
after applying Ducci operation will be vector in form ![]() (we can pull out the
(we can pull out the ![]() from all entries).
from all entries).
For example vector ![]() behaves exactly like
behaves exactly like ![]() . In the first case we get
. In the first case we get ![]() and in the second we get
and in the second we get ![]() and every vector is just 3 times the respective vector in the first case.
and every vector is just 3 times the respective vector in the first case.
After we prove all of this, we will try to concentrate more on length of a cycle. Informally said, cycle is a loop we get into. If we have ![]() , then we obtained cycle with length
, then we obtained cycle with length ![]() .
.
If we have binary vectors, we can view them as elements from module or vector space. We will need (and explain) knowledge about cosets, isomoprhism theorems and Cyclotomic polynomials