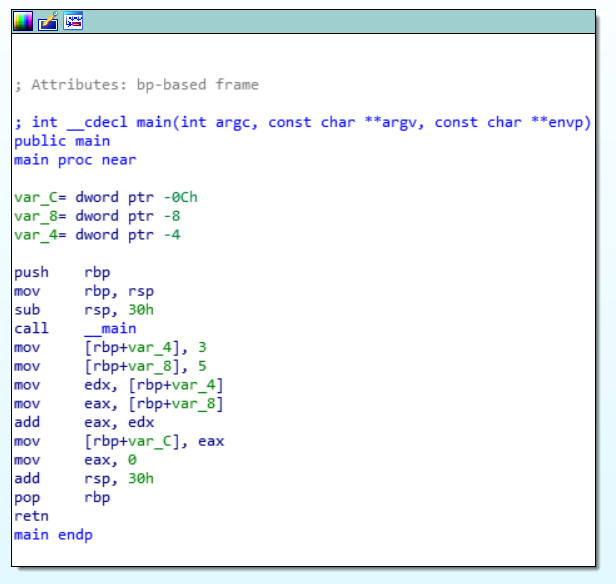
Okay, the second one is similar, needs one argument and then tells you it is incorrect if you try something random. I will try literally the same I did last time. I did fhx crackme02.exe > hex2.txt and just ctrl+f for Yes in this txt file. There is again
“Need exactly one argument..password1.No, %s is not correct…Yes, %s is correct!”
BUT password1 doesnt work this time! So I could find more about strings storage in exe, but looking at the hex and it rewritten to words
00002400 4E 65 65 64 20 65 78 61 63 74 6C 79 20 6F 6E 65 Need exactly one
00002410 20 61 72 67 75 6D 65 6E 74 2E 00 70 61 73 73 77 argument..passw
00002420 6F 72 64 31 00 4E 6F 2C 20 25 73 20 69 73 20 6E ord1.No, %s is n
00002430 6F 74 20 63 6F 72 72 65 63 74 2E 0A 00 59 65 73 ot correct…Yes
00002440 2C 20 25 73 20 69 73 20 63 6F 72 72 65 63 74 21 , %s is correct!
I guess I can calculate/compare hex numbers and letters/symbols and find out what %s refers to and find the address of it (the address is always written at the very left).
Looking at the last line, it seems 2C is a comma (and it is used before and again seems it is 2C), then 20 would be %… but 20 is used 3 times on 3rd line and only one %, huh. Lemme check the line in more detail
6F – o
72 – r
64 – d
31 – 1
00 – .
4E – N
6F – o
2C – ,
20 – (space)
25 – %
Ahh, so 25 will be % sign, i did not notice the space in the wordpad (in notepad++ i can now clearly see it lol). So %s is 25 73 here. I am not sure it refers to the memory of the given string though, or to some comparision, or just showing part of the code and translating it to hex numbers, or something totally else.
Part of the hex containing address 2573
00002570 54 68 65 20 72 65 73 75 6C 74 20 69 73 20 74 6F The result is to
00002580 6F 20 73 6D 61 6C 6C 20 74 6F 20 62 65 20 72 65 o small to be re
00002590 70 72 65 73 65 6E 74 65 64 20 28 55 4E 44 45 52 presented (UNDER
000025A0 46 4C 4F 57 29 00 55 6E 6B 6E 6F 77 6E 20 65 72 FLOW).Unknown er
000025B0 72 6F 72 00 00 00 00 00 5F 6D 61 74 68 65 72 72 ror….._matherr
000025C0 28 29 3A 20 25 73 20 69 6E 20 25 73 28 25 67 2C (): %s in %s(%g,
000025D0 20 25 67 29 20 20 28 72 65 74 76 61 6C 3D 25 67 %g) (retval=%g
000025E0 29 0A 00 00 E8 D5 FF FF 9C D5 FF FF 34 D5 FF FF )…èÕ..œÕ..4Õ..
I have literally zero idea about why is here the text about “The result…”. The exact byte on 2573 is 20, which is just space, so it seems this is not the way. No idea about the %s in %s(%g,%g) (retval=%g), not even sure what %g is for (placeholder for some datatype, as %s is for strings and %d for ints?)
I will look more into the hex and check if something looks like code or strings.
This is interesting
00005200 92 26 00 00 05 00 01 08 00 00 00 00 3A 47 4E 55 ’&……….:GNU
00005210 20 43 39 39 20 31 34 2E 32 2E 30 20 2D 6D 36 34 C99 14.2.0 -m64
00005220 20 2D 6D 61 73 6D 3D 61 74 74 20 2D 6D 74 75 6E -masm=att -mtun
00005230 65 3D 67 65 6E 65 72 69 63 20 2D 6D 61 72 63 68 e=generic -march
00005240 3D 6E 6F 63 6F 6E 61 20 2D 67 20 2D 4F 32 20 2D =nocona -g -O2 –
00005250 73 74 64 3D 67 6E 75 39 39 00 0C 18 00 00 00 00 std=gnu99…….
00005260 00 00 00 00 10 00 40 01 00 00 00 05 04 00 00 00 ……@………
00005270 00 00 00 00 00 00 00 07 01 06 63 68 61 72 00 24 ……….char.$
00005280 77 00 00 00 0A 73 69 7A 65 5F 74 00 04 23 2C 93 w….size_t..#,“
00005290 00 00 00 07 08 07 6C 6F 6E 67 20 6C 6F 6E 67 20 ……long long
000052A0 75 6E 73 69 67 6E 65 64 20 69 6E 74 00 07 08 05 unsigned int….
000052B0 6C 6F 6E 67 20 6C 6F 6E 67 20 69 6E 74 00 0A 75 long long int..u
000052C0 69 6E 74 70 74 72 5F 74 00 04 4B 2C 93 00 00 00 intptr_t..K,“…
000052D0 0A 77 63 68 61 72 5F 74 00 04 62 18 E5 00 00 00 .wchar_t..b.å…
000052E0 24 D0 00 00 00 07 02 07 73 68 6F 72 74 20 75 6E $Ð……short un
000052F0 73 69 67 6E 65 64 20 69 6E 74 00 07 04 05 69 6E signed int….in
00005300 74 00 07 04 05 6C 6F 6E 67 20 69 6E 74 00 05 77 t….long int..w
00005310 00 00 00 05 FB 00 00 00 07 04 07 75 6E 73 69 67 ….û……unsig
00005320 6E 65 64 20 69 6E 74 00 07 04 07 6C 6F 6E 67 20 ned int….long
00005330 75 6E 73 69 67 6E 65 64 20 69 6E 74 00 07 01 08 unsigned int….
00005340 75 6E 73 69 67 6E 65 64 20 63 68 61 72 00 05 53 unsigned char..S
I hoped after “masm=att” (which tells us what assembler is being used) i will see some code in assembly, but there are only data types (I guess it could be from some included header).
I quickly scrolled through all the 8500 lines, but didnt see anything interesting. Searching for “mov” (assembly keyword) did not help.
I know that at the beginning is lots of things defined and even addresses written (for example for where is the code stored), but there is almost nothing in text, there is only for example PE
50 45 00 00 64 86 14 00 6A FB B4 67 00 84 01 00 PE..d†..jû´g.„..
00000090 D0 06 00 00 F0 00 26 00 0B 02 02 2B 00 1C 00 00 Ð…ð.&….+….
000000A0 00 46 00 00 00 02 00 00 E0 13 00 00 00 10 00 00 .F……à…….
000000B0 00 00 00 40 01 00 00 00 00 10 00 00 00 02 00 00 …@…………
000000C0 04 00 00 00 00 00 00 00 05 00 02 00 00 00 00 00 …………….
000000D0 00 60 02 00 00 06 00 00 68 47 02 00 03 00 60 01 .`……hG….`.
000000E0 00 00 20 00 00 00 00 00 00 10 00 00 00 00 00 00 .. ………….
and then one has to know what the bytes mean (for example 64 86 is actually 86 64 and stands for the architecture, ie it is telling me the exe is for 64bit operation system).
Okay, if the code is obfuscated or something, I think I need to learn where to find strings/code, so I try to google it or ask chatgpt.
So it seems in the section .text (which is written on the right where begins, so I can find it ez), there are bytes for
.
t
e
x
t
then few zeroes
then four bytes for something, four bytes again, four bytes, and then finally four bytes for address for the code itself.
00000180 00 00 00 00 00 00 00 00 2E 74 65 78 74 00 00 00 ………text…
00000190 28 1A 00 00 00 10 00 00 00 1C 00 00 00 06 00 00 (……………
000001A0 00 00 00 00 00 00 00 00 00 00 00 00 60 00 00 60 …………`..
So it seems the address for code is 00 06 00 00, but it is stored in so called little endian format, so it is 0+6*100+0*1000+0*10000 (all numbers in hexa) = 600
Oh welp, it seems like the code indeed begins at 600, but for every assembly instruction there is a hex number. So it is not just commands rewritten to ascii, so there are no words
00000600 C3 66 66 2E 0F 1F 84 00 00 00 00 00 0F 1F 40 00 Ãff…„…….@.
00000610 48 83 EC 28 48 8B 05 35 34 00 00 31 C9 C7 00 01 Hƒì(H‹.54..1ÉÇ..
00000620 00 00 00 48 8B 05 36 34 00 00 C7 00 01 00 00 00 …H‹.64..Ç…..
00000630 48 8B 05 39 34 00 00 C7 00 01 00 00 00 48 8B 05 H‹.94..Ç…..H‹.
00000640 9C 33 00 00 66 81 38 4D 5A 75 0F 48 63 50 3C 48 œ3..f8MZu.HcP<H
00000650 01 D0 81 38 50 45 00 00 74 66 48 8B 05 DF 33 00 .Ð8PE..tfH‹.ß3.
00000660 00 89 0D A5 5F 00 00 8B 00 85 C0 74 43 B9 02 00 .‰.¥_..‹.…ÀtC¹..
00000670 00 00 E8 A9 18 00 00 E8 34 18 00 00 48 8B 15 8D ..è©…è4…H‹.
00000680 34 00 00 8B 12 89 10 E8 1C 18 00 00 48 8B 15 5D 4..‹.‰.è….H‹.]
00000690 34 00 00 8B 12 89 10 E8 84 05 00 00 48 8B 05 1D 4..‹.‰.è„…H‹..
000006A0 33 00 00 83 38 01 74 50 31 C0 48 83 C4 28 C3 90 3..ƒ8.tP1ÀHƒÄ(Ã
000006B0 B9 01 00 00 00 E8 66 18 00 00 EB BB 0F 1F 40 00 ¹….èf…ë»..@.
000006C0 0F B7 50 18 66 81 FA 0B 01 74 45 66 81 FA 0B 02 .·P.fú..tEfú..
So either I can go google what the relevant numbers mean and assemble (hehe) an assembly code. Or try more to look for the strings. I will begin with the strings.
It seems most often I should look at the .rdata
000001D0: [ Byte offsets relative to the start of this header ] Bytes 0x00-0x07: 2E 72 64 61 74 61 00 00 => “.rdata” (the section name) Bytes 0x08-0x0B: 50 0B 00 00 => VirtualSize (0xB50) Bytes 0x0C-0x0F: 00 40 00 00 => VirtualAddress (0x4000) Bytes 0x10-0x13: 00 0C 00 00 => SizeOfRawData (0xC00) Bytes 0x14-0x17: 00 24 00 00 => PointerToRawData
uld
000001D0 00 00 00 00 40 00 00 C0 2E 72 64 61 74 61 00 00 ….@..À.rdata..
000001E0 50 0B 00 00 00 40 00 00 00 0C 00 00 00 24 00 00 P….@…….$..
000001F0 00 00 00 00 00 00 00 00 00 00 00 00 40 00 00 40 …………@..@
00000200 2E 70 64 61 74 61 00 00 4C 02 00 00 00 50 00 00 .
so 2400
And that took me back where i began -__-
00002400 4E 65 65 64 20 65 78 61 63 74 6C 79 20 6F 6E 65 Need exactly one
00002410 20 61 72 67 75 6D 65 6E 74 2E 00 70 61 73 73 77 argument..passw
00002420 6F 72 64 31 00 4E 6F 2C 20 25 73 20 69 73 20 6E ord1.No, %s is n
00002430 6F 74 20 63 6F 72 72 65 63 74 2E 0A 00 59 65 73 ot correct…Yes
00002440 2C 20 25 73 20 69 73 20 63 6F 72 72 65 63 74 21 , %s is correct!
00002450 0A 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 …………….
00002460 50 16 00 40 01 00 00 00 00 00 00 00 00 00 00 00 P..@…………
00002470 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 …………….
00002480 00 A0 00 40 01 00 00 00 08 A0 00 40 01 00 00 00 . .@….. .@….
00002490 6C 70 00 40 01 00 00 00 38 90 00 40 01 00 00 00 lp.@….8.@….
I think I will have to try the code. I googled %g and I found it is either for float or for scientific notation.
I guess I could try to check what the “%s in %s(%g,%g) (retval=%g)” is for. Seems like it is in some printf, so probably not helpful either. So either googling for the numbers for the assembly instructions or trying to understand more how string references work.
So I decided to check the code. To be honest it would be best to just write a parser that checks through this. The problem of course is, I have no idea how to use powershell to do anything even remotely similar. So I will play with that.
This is syntax from help
Format-Hex [-Path] <string[]> [<CommonParameters>]
Format-Hex -LiteralPath <string[]> [<CommonParameters>]
Format-Hex -InputObject <Object> [-Encoding {Ascii | UTF32 | UTF7 | UTF8 | BigEndianUnicode | Unicode}] [-Raw] [<C
ommonParameters>]
Unfortunately I still have not much idea what it means, how to use the string argument. Something like “fhx .\crackme02.exe “a”” produces:
Format-Hex : A positional parameter cannot be found that accepts argument ‘a’.
At line:1 char:1
+ fhx .\crackme02.exe “a”
+ ~~~~~~~~~~~~~~~~~~~~~~~
+ CategoryInfo : InvalidArgument: (:) [Format-Hex], ParameterBindingException
+ FullyQualifiedErrorId : PositionalParameterNotFound,Format-Hex
The “a” is problematic. The thing I would need right now is to find a substring I choose. I know one can write whole programs in powershell, but no idea if I can discover it myself.
After a small thought I decided I want to google how to write scripts/code from powershell. Okay so, powershell runs files with extension ps1. Also looked for command to print out first 100 bytes, which is
Get-Content -Path .\file.exe -Encoding Byte | Select-Object -First 100 | Format-Hex
Well that was lots of googling (given the constraint this should be a rly hard challenge :D), so lets see what I can find out with help command. I can find out I will kill myself if I wont discover how the arguments work, there is again like 948398498 of those and idk how to use them. I see alias is “cat”, I will be using that. If I do “cat crackme02.exe”, it prints out the hex contents, but not hex numbers, rather the symbols, so lots of unreadable stuff and sometimes readable string. So I am not sure why to use it in the longer command, if I could use Format-Hex, will try.
Then there is -Path .\file.exe, so i suppose there I just write path to my file and then file. Also I suppose I can skip path if I am running powershell from the folder the exe is in (worked like that for fhx).
-Encoding Byte is almost surely for writing the hex numbers for the hex numbers, I suppose I could do “cat crackme02.exe -Encoding Byte”. And yes, it works, writes the numbers in decimal though. I suppose the Format-Hex at the end makes it into hex. Yea, cat crackme02.exe -Encoding Byte | Format-Hex just does the same as fhx crackme02.exe. I don’t understand much the | operator.
Hm, when I write only |, it writes >> at the beginning of the line, “pipe”. Example
>> f
At line:1 char:1
+ |
+ ~
An empty pipe element is not allowed.
+ CategoryInfo : ParserError: (:) [], ParentContainsErrorRecordException
+ FullyQualifiedErrorId : EmptyPipeElement
Oh i think I can pipe commands to other commands. So this Get-Content -Path .\file.exe -Encoding Byte | Select-Object -First 100 would be taking the get-content command and passing it to select-object, in other words would be something like, if we wrote it as composing of functions: Select-Object – First 100 (Get-Content …)